2）凸空间的表现形式

      建筑空间的另一种句法表现形式是凸空间地图。离散凸空间通过将布局的空间复杂性降低到最少最胖的凸空间来表示邻接关系。在每个凸空间中，所有的点对都是可见的。相邻的空间之间将有一个“depth”，间隔最少一个空间的两空间之间将有两个“depth”，以此类推。换句话说，两个空间之间的“depth”被定义为图中从一个空间移动到另一个空间所需的最少的句法步骤或最短的拓扑距离。

      我们可以将拓扑深度的价值归结于邻接图G中的每个节点(顶点)。图G由两套信息组成：图顶点(表示凸空间）Vc={Vc1,Vc2,……Vcn}和一组线La ={La1,La2……Lal}，图G中的每一条线表示凸空间与凸空间之间的邻接关系。空间邻接关系是表征结构在空间布局中如何配置的基本关系。在对偶图G中，两个空间i和j被认为是相邻的:当可以从一个空间直接访问另一个空间，而不需要通过中间的空间。凸空间表示的数学描述方法与轴向网络相似。

      图2.3展示了Frank Gehry使用凸空间表示来解码建筑布局的示例。建筑空间(a.)可以用最小最胖的凸空间集合来表示。这些空间是连接的，其中有一个空间直接访问到另一个空间，由此形成了一个凸空间地图（b)，然后凸空间再由一个图(c)表示，每个顶点的不同连接性(度)值被突出显示;与邻近点有更多连接的顶点将具有更高的连接性值(d)，这些连接度值随后在凸空间地图上显示，以揭示建筑组织的空间结构(e)。

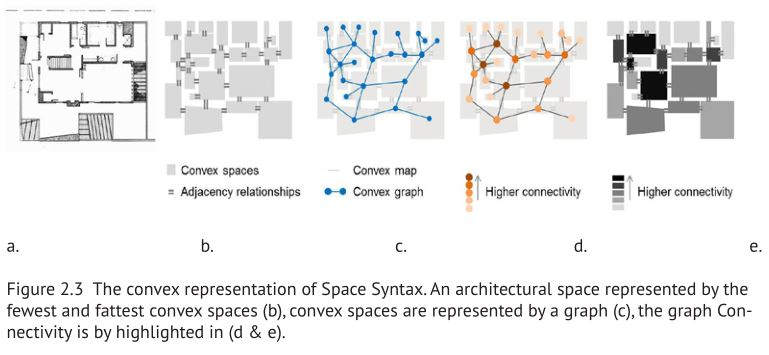
图2.3空间句法的凸空间表示。一个建筑空间由最小最胖的凸空间(b)表示,凸空间再由图(c)表示，图形连接度由(d和e)突出显示

      布局中相邻空间之间的空间关系可以用justified graghs来表示，这种图最早由希利尔和汉森(1984)提出。它将凸空间的空间网络从一个空间(根)读取到所有其他空间：用圆形表示每个凸空间，用直线表示两个空间之间的每个可渗透连接，如图2.4所示。在根空间中，所有离根空间一步远的空间都放在根空间之上的第一级，所有离根空间两步远的空间都放在第二行，以此类推。一个justified graghs可能是深的，也可能是浅的，这取决于根空间与其他空间的关系。空间关系可能形成分枝树或环形。两个空间之间的空间关系可能是对称的，例如:“A连接到B”等于“B连接到A”。否则,这种关系就被认为是“不对称的”。平面图中从任何一点开始的不对称总虽与从该点开始的平均深度相关，以其“相对不对称”(RA)来衡量。总的来说,空间上最接近所有空间(低 RA)的空间在空间网络中是最完整的。由于它们在空间网络中的中心位置，它们的特点是提供密集的交通。位于更深位置(高RA)的空间隔离程度最高。整合和分离是空间网络的全局属性。

      空间布局通常是分层结构和运动环的组合。通常情况下，空间的树状结构反映了一种深层的、受控的空间结构，也许还反映了建筑中社会组织的层次结构。相反,在布局中提供相互连接的运动环，就提供了移动路线的选择，减少了空间的深度。每个凸空间的空间类型因其与运动环的关系而不同(图2.4)。

Hillier教授(1996)区分了四种类型的空间:

●a型：被描述为终端空间，并在图中连接不超过一个空间

●b型：连接图中的两个或多个空间，而不属于任何运动环的一部分。

●c型：通常位于一个运动环上。

●d型：空间必须位于连接两个或多个环的连接处。

      a、b、c、d类型的空间在整个网络的局部和全局设置内的定位可以决定布局的整体空间步深。局地增加a型空间和在全球范围增加d空间将最终减少空间步深,并形成一个集合整体的系统；而全球性增加b型空间和局地增加c型空间可能会导致步深的最大化,导致形成隔离系统。

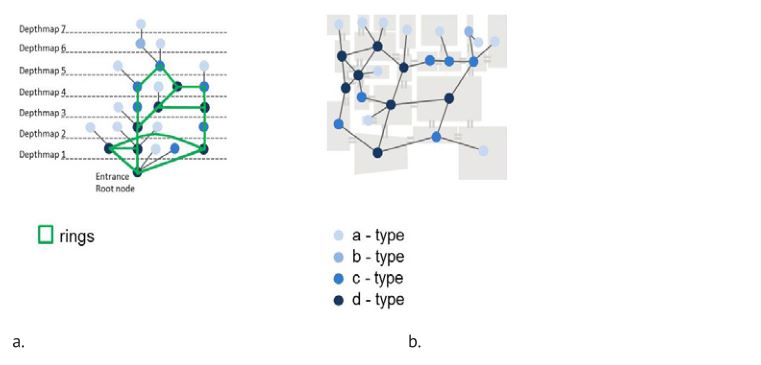
图24在凸空间关系图上标出的不同空间类型。两个图表分别是：从弗兰克.盖里(Frank Gehry)住宅的外部与内部连接点开始的一个调整图(a)、一个覆盖在凸空间地图上的邻接图(b)。

      Justified graghs的表示格式可以应用于轴图和凸空间图。轴向图的环度是区分街道网络秩序和结构模式的关键。为了量化这些性质，在(Hillier & Hanson, 1984:91)中提出了轴向图的轴向度量;即轴向图中电路/环与轴向线数的比值。网格轴向可遵循以下公式

      网格同轴度=[(I+2)+2]/L

      其中I是岛的数目，L是轴线的数目。结果在0和1之间变化，高值接近规则网格，低值接近轴向变形系统。