Introducing random walk measures to space syntax

在空间句法中引入随机漫步测度

Abstract

We introduce Random Walk Closeness (RWC) to the space syntax computational paradigm. Random walks are stochastic processes in which an unbiased walker traverses a network purely based on his current location. Random walks have been used by space syntax in an agent based scenario, where results are simulation based. Here, the results are mathematical based, i.e. RWC is derived from access times, which are the average number of steps it takes to walk between locations. Results suggest an improvement in correlating pedestrian movement over Integration, RA and network Closeness.

摘要

在空间句法计算范式m中，引入了随机漫步接近度(RWC)。随机步行是一个无偏步行者纯粹基于其当前位置穿越网络的随机过程。在基于agent的场景中，空间语法使用了随机m步，其结果是基于模拟的。在这里，结果是基于数学的，即RWC来自访问时间，这是它在位置之间行走的平均步数。研究结果表明，行人运动的相关性优于整合、RA和网络的紧密性关键字随机行走，访问时间，积分。1. 介绍随机游动的概念一直被空间句法方法(如积分和选择)所暗示，但没有得到充分的探讨。然而，这个概念在网络分析和数学的其他领域的相关工作中是中心的。本文investiçates研究了城市图中随机游动的性质，旨在建立这些性质之间的桥梁，有助于更好地理解空间句法度量。

Keywords

Random walk, access times, integration.

关键字

随机漫步，访问时间，融合。

1. 介绍

随机游动的概念一直被空间句法的度量所暗示，如积分和选择，但没有得到充分的明确探讨。然而，在网络分析和数学的其他领域，它是一个核心的概念。本文对城市图中随机游动的性质进行了研究，以期在此基础上对城市图中随机游动的性质进行联系，并对空间句法度量的基本理解有所帮助。

随机游动的直觉类似于空间语法中测量的图的结构属性。在积分的情况下，它首先是路径的度量。整合在形式上是图本身的属性(如深度)，但其重要性通常被描述为图中的行动属性，例如:从一个节点移动到另一个节点所需要的“回合数”。深度被用作可接近性的指标。在实证观察的背景下，通常会对记录的数据进行整合，以证明在特定空间中观察到的行人或车辆密度越大，整合值越高。

这再次暗示了静态图与单个路径的关联其次，假设这些路径是随机的，这反映了大量不同人群的概念，而不是单个人。关键的衡量标准是平均深度，它是从每个其他节点的总和中考虑的，因此假设单个路径的细节并不重要，但因为这些是独立的，单个路径目标随机分布在整个种群中，大数定律表明，在所有路径的总和中，人口的分布将可靠地收敛。如果空间语法偶尔被批评为屈从于空间决定论，那么错误的地方在于对个体差异和集体可靠性之间的差异的误解。

在空间的视觉代理模拟中，空间语法有意地使用了一种特定类型的随机行走(Turner和Penn, 2002)，其中每个代理的运动是由每个时间步上的随机选择方向驱动的  显然，这样的智能体路径并不能单独代表人类的运动，但许多智能体在空间中的聚集分布可以代表人类的运动。正是这种聚合行为可靠地受到图所代表的空间的影响，通过空间svntax措施的集成和选择被认为是该图的一个属性。

其他相关领域，包括数学图论和应用较多的网络工程，明确地使用了随机游动的计算。这些也可以证明收敛于一个稳态分布随时间;然而，这种分布可以通过解析来确定，而不需要迭代模拟。轴向地图及相关表征已经被数学家使用如布兰查德和Volchenkoy(2009),他特别提到空间句法和捕获分析城市图,但即使在这种情况下的基本方法分析不整合或选择,但随机漫步。

这两种度量都与纯图和网络理论中度量的中心性有关，集成近似中心性，选择近似中心性。它们是很相似的度量，但与它们的定义不同，特别是在空间句法研究中，它们被细化为城市图的细节。它们在实践中被使用，部分原因是它们已被证明可以解释大量的经验观察结果，因此，任何替代测量方法都可以与相同的经验观察结果进行有益的比较。本文回顾了一种基于随机步行的中心性计算方法——随机步行近度(random walk close, RWC)，并将其与两个社区知名的城市案例的整合进行了比较。这些结果表明RWC与观察的相关性优于与整合的相关性。

在回顾案例研究的结果之前，以下部分将通过对亲密度和首次通过时间的数学描述介绍随机行走亲密度的度量。

2. Closeness in a graph

A graph consists of a node (or vertex) set often notated by V, and an edge (or arc) set notated by E, which is a binary relation on V. If E is a symmetric relation then G is called an undirected graph. A network centrality is a function defined on V which assigns importance to nodes according to certain criteria.

Closeness is one of the earliest network centralities, introduced by Bavelas (1950), and later refined by Beauchamp (1965). Given a connected network, represented as an undirected graph G = (V, E), with no self loops or multiple edges, the Closeness of a node V is defined as: 

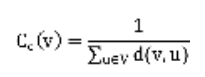
Where d(v, u) is the length of the shortest path from node v to node u.

Closeness, thus defined, is used in the calculation of Integration, and RWC also averages values over all possible steps it takes to reach a node. In integration this is treated as a direct measure of the graph; in RWC as a means to determine probabilities of random movement occurring at a node.

2. 图的封闭性

一个图由一个节点(或顶点)集和一个边(或弧)集组成，它们通常用V来表示，E是V上的一个二元关系。如果E是一个对称关系，则G称为无向图。网络中心性是定义在V上的一个函数，根据一定的准则赋予节点重要性。

亲密性是最早的网络中心性之一，由Bavelas(1950)引入，随后由Beauchamp(1965)提炼。给定一个连通网络，表示为无向图G =(V, E)，无自环，无多条边，节点V的封闭性定义为: 

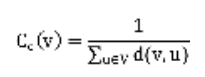
1C（v）=uvd（vu其中d(v, u)是节点v到节点u的最短路径长度。

这样定义的贴近度在Integration的计算中使用，RWC也在到达一个节点的所有可能步骤中取平均值。在积分中，这被视为图的直接度量;在RWC中，作为一种手段，以确定随机运动的概率发生在一个节点。

3. From graphs to Markov chains

The underlying random walk based on a given graph (such as the axial or segment graphs), is most easily represented using an object called a Markov chain. Its construction for a particular graph is quite simple, as illustrated in Figure 1. A star of 4 nodes is transformed into a Markov chain by duplicating each edge bidirectionally and assigning edge weights. The edge weights are assigned uniformly based on the degree of each node. The weights represent the probabilities of a walker moving to adjacent nodes from a given node, and are called transition probabilities. Clearly, in the case of a star the transition probability from each leaf (node with degree 1) to the center is 1. Therefore the average walking time (number of steps) from a leaf to the center is 1. But what of the opposite? What is the average time it would take to walk from the center, u, to a leaf v? We may represent this time in an equation. Denote the time H(u ,v), then in the case of the star in Figure 1:

H(u,v)=1/3×1+1/3×(H(u,v)+2)+1/3×(H(u,v)+2)=1/3+2/3×(H(u,v)+2)

The term (H(u,v)+2) means that if we walk to another leaf other than v then we are sure to return to the center at the next step, meaning that 2 is added to the overall time. This reflects an important property of Markov chains, that they are memoryless, i.e. if the walk returns to a node after a while then the probabilities from that node are identical regardless of the time that has past.

Therefore from the equation above, 1/3 H(u,v)=5/3, giving H(u,v)=5.

So walking from a leaf to the center would always take 1 step, while walking from the center to any specific leaf would take an average of 5 steps.

Figure 1: A star graph of 4 nodes transformed to a Markov chain.

3. 从图到马科伊链

基于给定图(如轴向图或分段图)的底层随机游走最容易使用一个称为Jarkoy链的对象来表示。它对于特定图的构造非常简单，如图1所示。通过对每条边进行双向复制并赋予边权值，将4个节点的星形转化为马氏链。边缘权值是根据每个节点的度进行统一赋值的。权值代表了步行者从给定节点移动到相邻节点的概率，称为转移概率。Clearlv，在星形的情况下，从每个叶(节点)的转移概率到中心的度1)是1。因此，从叶子到中心的平均行走时间(步数)是1。但反过来呢?从中心u走到叶节点v的平均时间是多少?我们可以用方程表示这个时间。表示时间H(u,y)，则对于图1中的星号:

H(u,v)=1/3×1+1/3×(H(u,v)+2)+1/3×(H(u,v)+2)=1/3+2/3×(H(u,v)+2)

(H(u,v)+2)表示如果我们走到v之外的另一片叶，那么我们肯定会在下一步回到中心。这意味着总时间增加了2。这反映了马尔可夫链的一个重要的r属性，即它们是无记忆的，也就是说，如果行走一段时间后返回到一个节点，那么该节点的概率与过去的时间无关。

因此，由上式可知，1/3 H(u,v)=5/3, giving H(u,v)=5.

所以从叶子走到中间总是要走1步，而从中间走到任何特定的叶子平均要走5步。

4. 通过谱分解的首次通过时间

真实的网络比给出的星型网络要大得多、复杂得多。然而，对于任意一对节点u, v，有一种方法可以精确计算首次通过时间H(u, v)，这是基于一个称为拉普拉斯矩阵的谱分解，该矩阵是基于给定网络的马尔可夫链的转移矩阵。在本质上所示的计算是类似的明星,但很容易看到,一个更大、更复杂的网络计算不会那么简单,但是有一个公式H (u, v),使用上面提到的拉普拉斯算子矩阵的特征向量和特征值。

5. 首次通过时间和RWC

从形式上讲，用d(v)表示v的节点度，用n(v)表示v的平稳分布值，即n(v)=(d(v))/(21E 1)。设M为图G上的马尔可夫转移矩阵，设d为一个对角矩阵

D (i) -1/(D (i))，我们定义标准化拉普拉斯T为:

T=D^(-1/2) MD^(1/2)

其中M是G上的标准随机游走转移矩阵。

让{1…N}是T的实特征向量的集合，设u 1…L N为T的实特征值从节点i到节点i的平均首通过时间为从节点i出发到达节点i所需的平均步数，由 

详细的概述和证明见(Lovász, 1993)。

随机行走接近(RWC)是在(Noh JD, 2004)中引入的。RWC使用到节点的平均首次通过时间来表示节点的重要性。

对于节点v, RWC值定义为:

C_RWC (v)=N/(∑_(u∈V)▒〖H(u,v)〗）

请注意，在这种情况下，平均首次通过时间通常相当于积分中的平均深度概念，但距离不是对称的。访问时间可以分析两个地方之间的关系，不仅基于网络距离，还基于从另一个地方到达一个地方所需的平均时间。在平均深度下，假设最短路径，而在平均初通过时间下，最短路径为随机路径。这使得我们能够在考虑整体网络效应的同时，不对称地理解一个地方与另一个地方的关系。缺点是RWC需要更长的时间来计算，但一旦计算出访问时间矩阵，数据就可以用于各种分析。

6. 案例研究:巴恩斯伯里和肯辛顿

在两个案例研究中，将RWC的测量与整合进行了比较，以了解其与整合的一般区别，并确定其与实际观察的相关性。由于RWC的计算时间较长，在第一次研究中决定使用轴向图而不是线段图，因此将重点放在积分上作为比较。为了便于与之前的研究(Hillier B, 2005)进行比较，选择了伦敦的Barnsbury和Kensington两个街区，从中可以获得与轴线相关的行人和车辆运动的样本数据。这些数据包括轴向图和特定样本位置(门)的MPH(每小时运动)。分配给轴线的实际MPH值是连接到原始数据中的每条线的门上的平均MPH值。

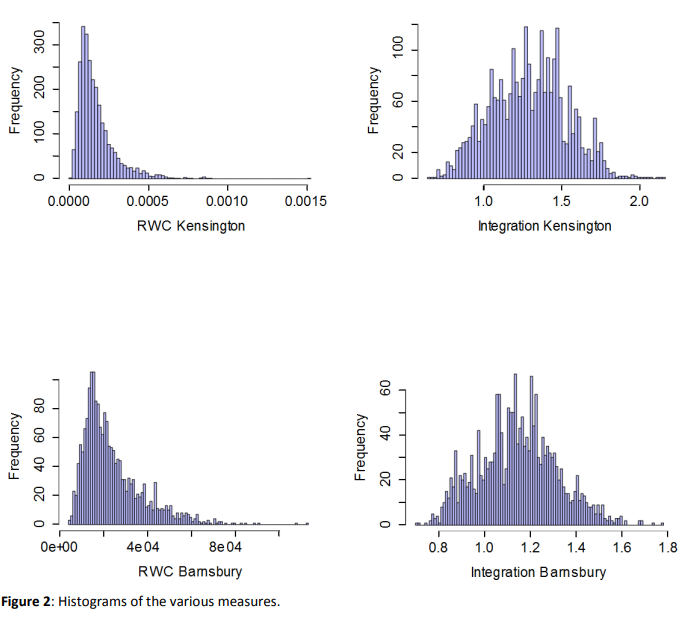
我们第一次RWC比较值的分布和集成措施本身,通过绘制直方图的这些两个街区(图2)。在这方面,我们希望的主要区别概念图深度和随机漫步的首次通过时间是明显的。正如上面星图所指出的，这些时间是不对称的，导致从中心到周长节点的距离(5步)比从周长到中心的距离长得多。我们可能会看到，与中心动脉相比，构成城市图背景的外围节点的值范围要低得多。直方图准确地显示了这一点，RWC的分布偏向于较不中心的节点，以及较中心节点的更细的尾部，而集成通常遵循一个更对称的分布。

然而，除了这种分布变化之外，轴向图本身在RWC和integration之间显示出显著的相似性。对巴恩斯伯里的分析包括了一个充足的周边边界，包括摄政公园到金斯兰路，肯辛顿包括所有海德公园周围的社区，从泰晤士河以南。在这两种情况下，特定街道的排名在两种方法下都是相似的，最明显的是在轴线上确定的最高整合或rwc -在两种情况下是相同的。

地图看起来不同，但主要是由于总体值的分布，而不是街道之间的特定差异。如上所述，不同的分布导致RWC在图中只有少数几条线在图中红色/橙色表示的高范围内，而大部分的地图在低得多的蓝色值内。少数轴线在最高范围内的区别更为明显。虽然更对称的整合分布更适合一个规则的，均匀的，颜色光谱，绘图可以通过改变这个颜色范围的映射更清楚。

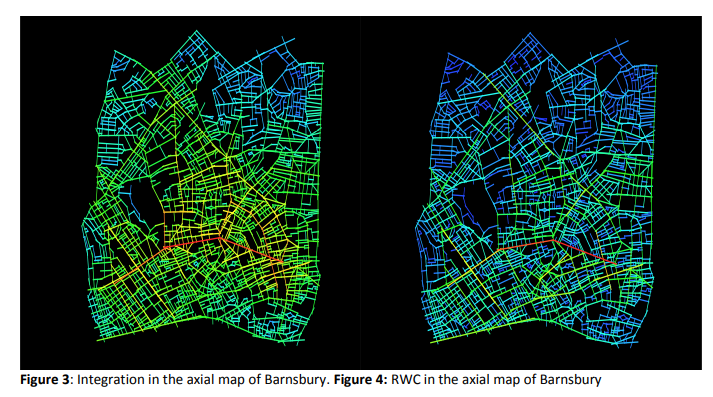
比RWC与一体化的关系更重要的是一体化解释了什么。当RWC测量被用作实际运动的预测时，它们似乎比整合行人和车辆数据的相关性更好。表1。列出了在巴恩斯伯里和肯辛顿的RWC和整合与观察到的行人和车辆运动之间的皮尔逊相关分数。原始相关性和对数/对数尺度的相关性都显示出来。在所有情况下，都有显著的改善，相关性平均提高了20%(两个社区的RWC的对数/对数(综合RWC的均值R=0.663, RWC的均值R= 0.797)。它们的散点图如图7和图8所示。

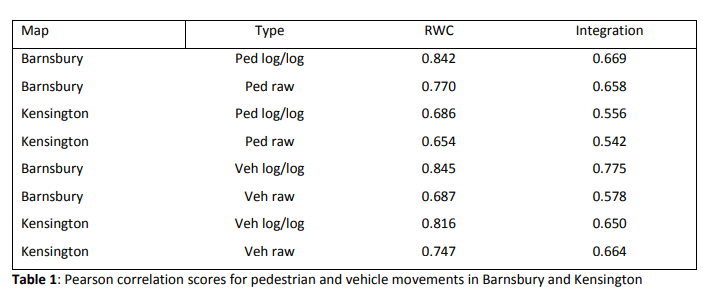
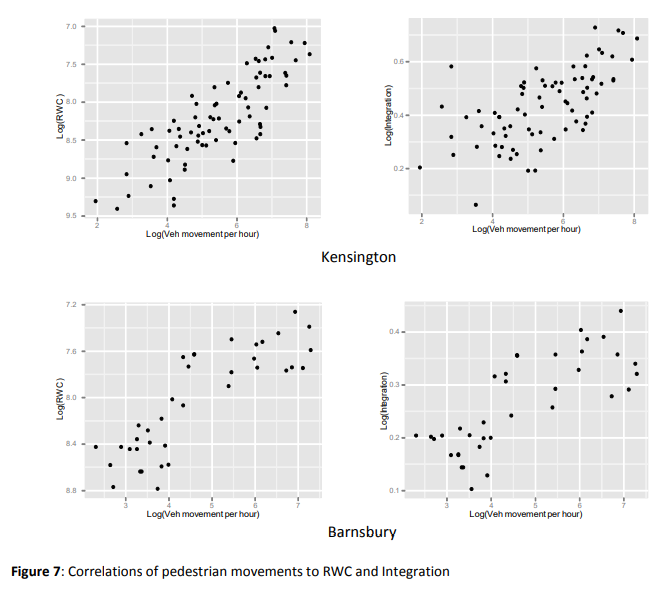
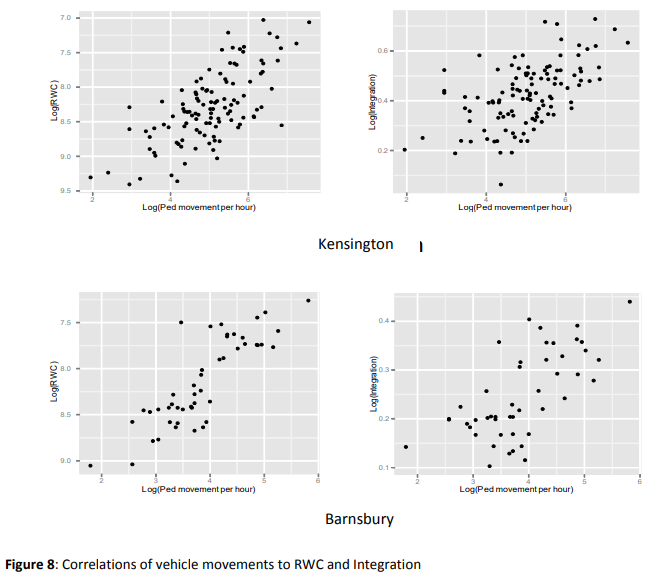
7. 讨论

在积分和RWC的度量之间有几个显著的区别，无论是关于被度量的是什么，还是在这样做的算法。由于随机漫步中出现连接较好的节点的概率显著增大，因此相邻节点之间的首次通过时间可能比平均深度相差更大，因此RWC的结果从一个节点到下一个节点的连续性应该会更小。当旅行社遇到高度节点时，会影响后续的步行。

这与上面提到的不对称性有关。当图中两个节点之间的深度从x到y和从y到x是相同的，随机遍历意味着一个更中心的节点比同一个外围节点从中心出现的距离“更近”。一个特定的位置与x的距离可能比与y的距离要远一些。在击中时间矩阵中，我们可以很容易地发现其中的细节，这可能会揭示图中特定位置的较大的不连续点。使这个矩阵可用可能会产生一个非常有用的附加分析工具。

计算测量值的算法的计算复杂度不同，这可能使RWC在不同条件下的计算比积分更不实用。让第四| = N。集成需要节点之间的距离。到一个特定节点的距离可以用O(IE log(N))来计算，因为我们处理的图是稀疏的，所以是O(Nlog(N))。对于整个图，其理论计算复杂度为O(N^2 log(N))，尽管在实践中，积分是通过一种比这更快的流算法来计算的。另一方面，RWC需要拉普拉斯矩阵的谱分解，这是一项繁重的计算任务。这意味着我们需要找到N个特征向量和特征值它们的时间复杂度是O(N^3)

本文重点讨论了轴向图中积分和RWC的比较，但也展示了其他几种直接的可能性。首先，RWC不是唯一存在的随机漫步测度;中间性中心性存在一个随机游走版本，它可能显示出对选择的类似改进。其次，为了与取样数据对应于轴线的现有案例研究进行比较，RWC应用于轴线，而不是线段图。计算同样可以以其现有的形式应用于段映射或任何其他图形表示，但明显的问题是，由于节点数量较多，段表示的计算时间要比轴表示的计算时间长。此外，在接近RWC的情况下，可以计算更少的特征值和特征向量，从而降低时间复杂度。这既需要对这种近似方法的准确性进行数学证明，也需要对其性能进行经验证明。

8. Conclusion

Random walk measures are related in general principle to the phenomena explained by existing space syntax measures, and are supported by significant research both theoretical (mathematics) and applied (engineering), but less so in the context of urban and other spatial networks. The wealth of observed data in these domains has to date primarily been described by the space syntax measures. This study has aimed to bridge the two. Comparing integration with RWC indicates strong similarities between the two measures, but the analysis of actual data suggests that RWC is a better approximation to observed pedestrian and vehicular movement.

 For the overall picture of the city given by the two measures, there is a rough equivalence in results: there is a similar ranking of more and less central street lines, as seen in the plots of the axial maps by integration and RWC values, albeit with different overall distribution. Many of the conclusions that would be drawn, such as the location of the city core, the deformed wheel pattern, etc. would be identical, and this equivalence could potentially put a great deal of previous spatial research on a firmer footing with respect to mathematics and related theory.

The use of RWC, as proposed here, does appear to result in improved correlation to the empirical data, so it is potentially a better way of explaining such observations in future research. If this continues to hold, the notion of the random walk itself, as a conceptual can descriptive tool, may help to provide a better means to understand and explain what occurs in the natural movement through space.

9. 结论

随机步行测度一般与现有空间句法测度所解释的现象相关，并得到了大量理论(数学)和应用(工程)研究的支持，但在城市和其他空间网络环境下的研究较少。迄今为止，这些领域中观测到的大量数据主要是通过空间语法度量来描述的。这项研究旨在架起两者之间的桥梁。将其与RWC进行比较，可以发现两者之间有很强的相似性，但对实际数据的分析表明，RWC更接近于观察到的行人和车辆运动。

对于这两种度量方法给出的城市总体情况，结果大致相当:从综合和RWC值得出的轴向图的图中可以看出，中心街道线的增多和减少的排序是相似的，尽管总体分布有所不同。得出的许多结论，如城市核心的位置、变形的车轮模式等，将是相同的，而这种等效性可能会使大量之前的空间研究在数学和相关理论方面建立一个更坚实的基础。

RWC的使用，正如本文所建议的，似乎改善了与经验数据的相关性，因此在未来的研究中，它可能是解释这些观察结果的更好方式。如果这种情况继续下去，随机行走的概念本身，作为一个概念性的描述性工具，可能有助于提供一个更好的方法来理解和解释在空间中的自然运动